(Astro)Physics of the Earth system

Week

GEOS 3410

πŸͺ‘

Week Schedule

Tuesday

  1. Wrap-up Earth system
  2. States of matter and energy
  3. Electromagnetic radiation

Thursday

  1. EM, cont.
  2. Orbits & obital cycles
  3. The Sun & solar variability

Outside of class

  • Complete/self-grade quantitative skills packet & meet with me, by Friday
  • Lab 1 due 11:59 pm on Friday

States of matter

Sensible & latent heat

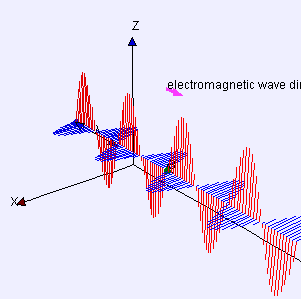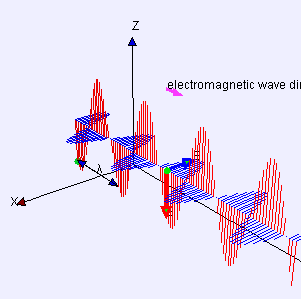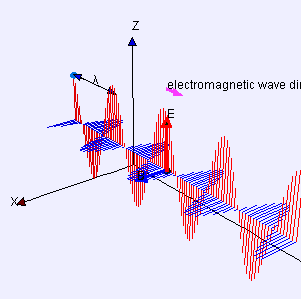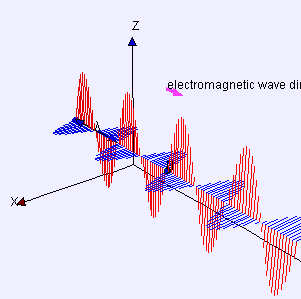
Electromagnetic Radiation

Electromagnetic Radiation

Behaves both like a …

  • wave: wavelength (λ), frequency (f)
  • particle: photons with discrete energy, E

\[\begin{aligned} \text{speed of light}~~ (m/s) \qquad c &= \lambda f \\ \text{energy}~~(J) \qquad E &= hf \\ \end{aligned}\] $$ \text{where} \qquad c = 3 \times 10^8~\text{m/s}, \qquad h = 6.67 \times 10^{-34}~\text{J~s} $$

Electromagnetic spectrum

Wikipedia

Electromagnetic wavelengths you should know

Type/region λ range λmin (m) λmax (m)
Ultraviolet 10 – 400 nm 10−8 4×10-7
Visible 400 – 700 nm 4×10−7 7×10−7
Infrared 0.7 – 1000 µm 7 ×10−7 10-3

Behavior of light

Thermal radiation

An idealized scenario: the physical blackbody

Perfect absorber absorbs all incident radiation (α=0)
Ideal emitter emission depends only on temperature
Diffuse emitter emits evenly in all directions

Blackbody emission is a fuction of temperature

Wikimedia

Total flux

(Stefan-Boltzmann law) \[\begin{aligned} F = \sigma T^4 \end{aligned} \]
… where $\sigma \approx 5.67 \times 10^{-8}~\text{W}~\text{m}^{-2}~\text{K}^{-4}$ (Stefan-Boltzmann constant)
Wikimedia

Peak wavelength of emission

(Wien's displacement law) \[\begin{aligned} \lambda_{max} = \frac{b}{T} = \frac{0.0029~m\cdot K}{T} \approx \frac{3~mm\cdot K}{T} \end{aligned} \]
Wikimedia

Why do we care about thermal emission?

Calculate the peak wavelength of blackbody emission for …

  1. The Sun: T = 5600 K ≈ 6000 K β˜€οΈ
  2. Saturn: T = 135 K ≈ 150 K πŸͺ
  3. Earth: T = 288 K ≈ 300 K 🌏
$$ \lambda_{max} = \frac{b}{T} \approx \frac{3~mm\cdot K}{T} $$

What happens to thermal emission when we warm an object?

Planck response

Spheres, radiation, and space

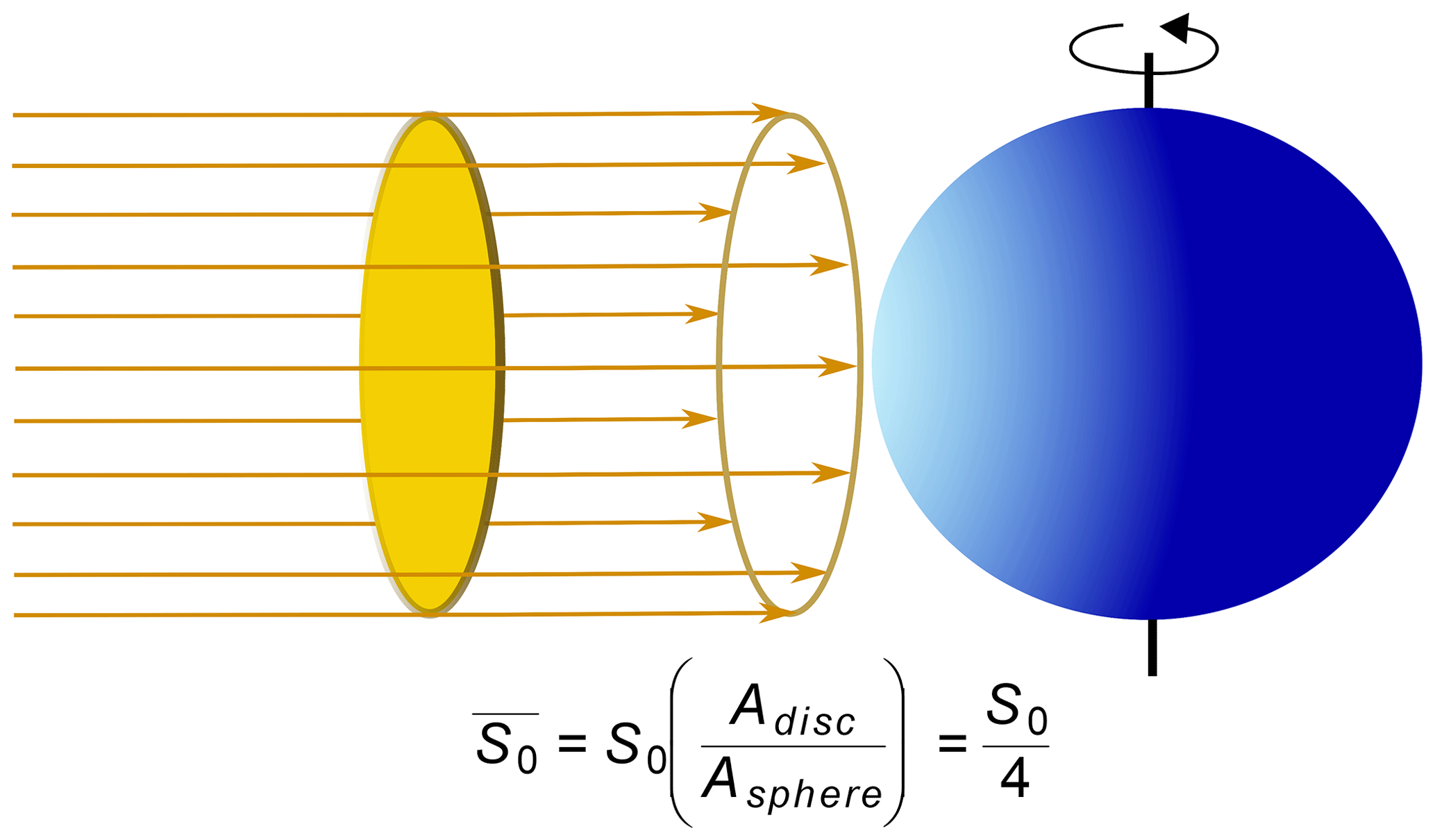
Spheres, radiation, and space

The solar radiant flux (W/m2) at a given distance d from the Sun's core is the solar luminosity L (W) spread over the area of a sphere.

How does incident flux $F$ scale with distance $d$ from the Sun?
$$F \propto \frac{1}{d^2}$$
Inverse square law
Oliveira, 2023

The solar constant

The solar flux at the top of Earth's atmosphere: $$G_{SC} = 1361~\text{W}~\text{m}^2$$ But, the average insolation of Earth's surface is ~340 W/m2
\[\begin{aligned} A_{disc} & = \pi r^2 \\ A_{sphere} & = 4 \pi r^2 \end{aligned}\]

Distribution of insolation

COMET / MetEd / UCAR, via Giannotti 2013

Orbits & orbital cycles

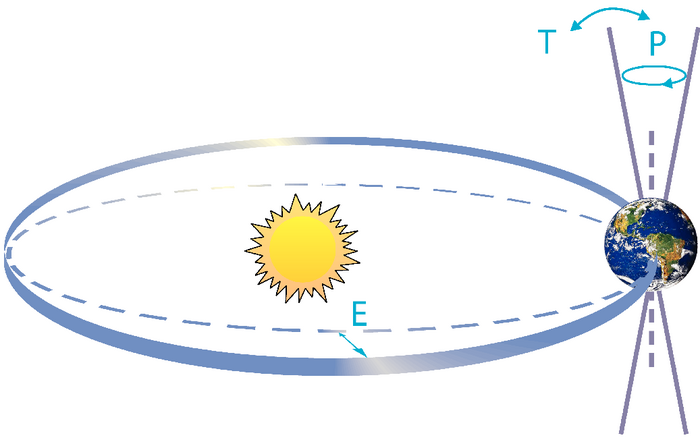
Planets (like Earth) orbit about their star and rotate about a spin axis.

Wikimedia

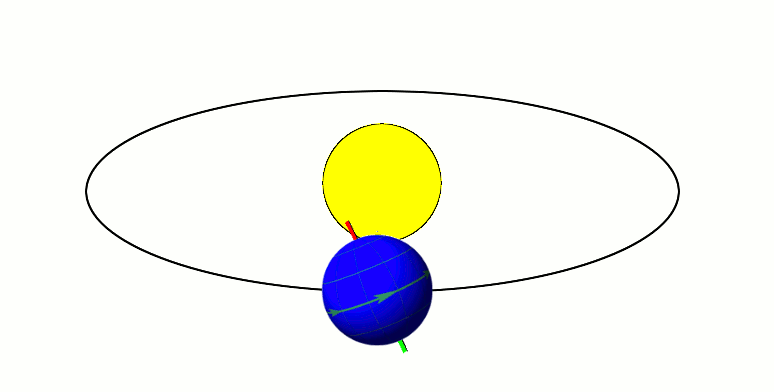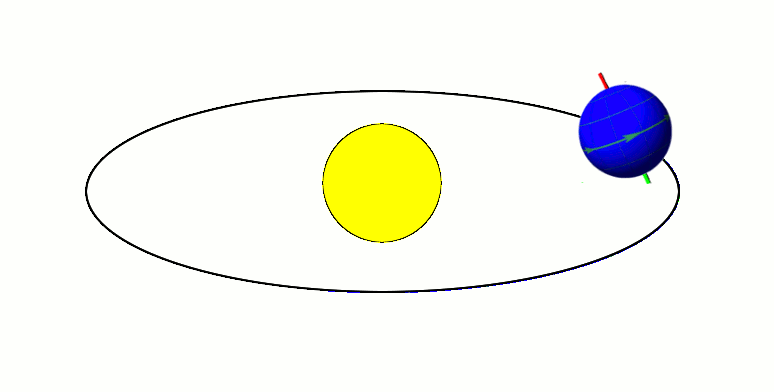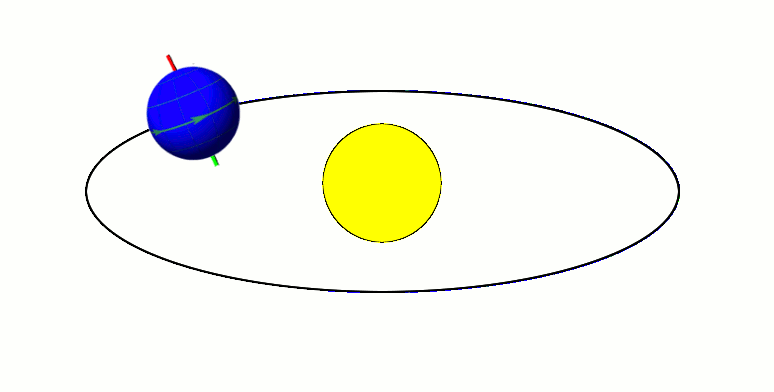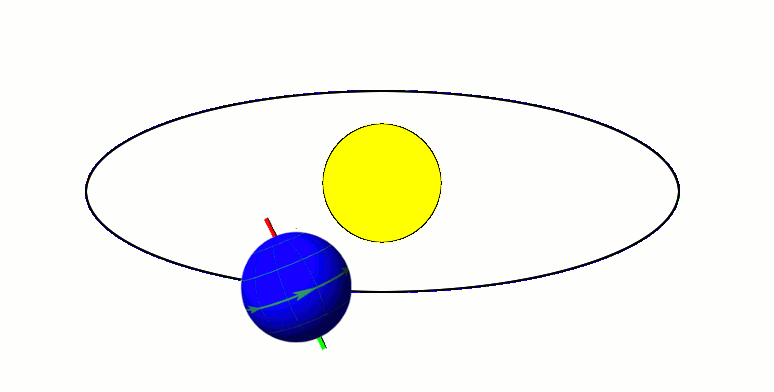
Axial Tilt / Obliquity

Current obliquity ~ 23.5°
Wikimedia

Tilt, Tropics & Circles

Wikimedia

Obliquity and precession cycles

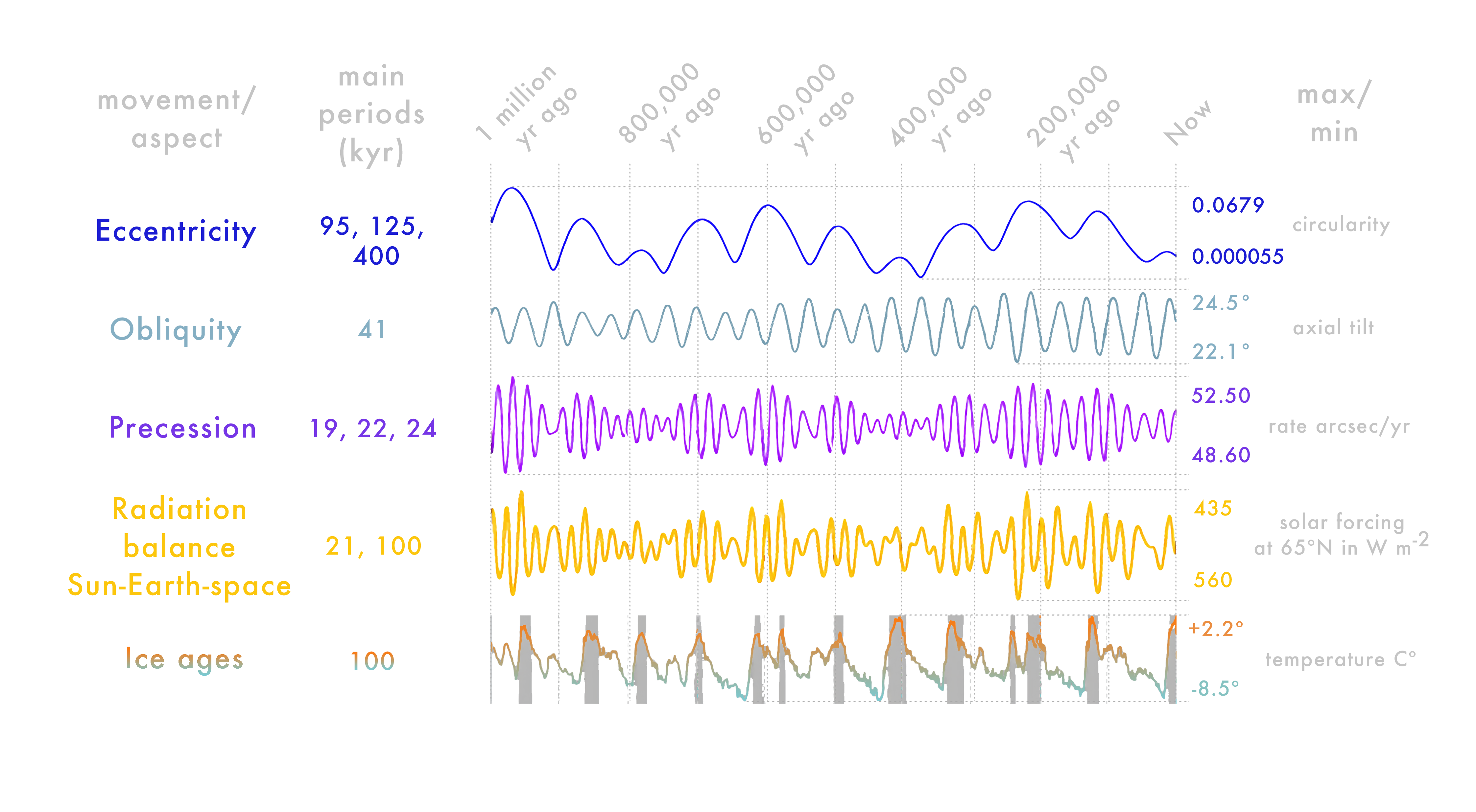
Obliquity: 41 kyr period, 22.1–24.5°
Axial Precession: 26 kyr period

Elliptical orbits have eccentricity


circle → e = 0      line → e = 1

Current e = 0.0167
Wikipedia: Ellipse, Earth's orbit

Eccentricity cycles

Periods: 95 kyr, 124 kyr, 405 kyr
(mostly interactions with Jupiter and Saturn)

Milankovitch (orbital) cycles

Cycle Effect
Obliquity Seasonality – warmer/cooler winters and summers
Eccentricity Duration of seasons,
Insolation at perihelion & aphelion.
Precession Timing of seasons (relative to perihelion)
IPCC AR4, WGI (2007)

Milutin MilankoviΔ‡ crunched numbers on insolation (1910–1940)

Mean insolation at 65°N

La2010

Why do we care?

Quasiperiodic (periodic-ish) climate cycles
Lisiecki & Raymo 2005

Spectral analysis of orbital records

Hays, Imbrie, Shackleton 1976

Spectral analysis of climate records

Hays, Imbrie, Shackleton 1976

All together now!

Wikimedia

Cluster Reflection Time!

  1. Why can't orbital cycles account for modern climate change?
  2. Orbital cycles typically cause minor changes in insolation. So how can they drive glacial-interglacial cycles?
  3. Why do we care so much about the Northern Hemisphere?
  4. Glaciers (ice sheets) form from the accumulation of ice over many years. What will have a larger effect — colder winters or colder summers?
  5. Lingering questions.
Gowan+ 2021

The Sun

Solar Dynamics Observatory

The Sun

Solar structure

  • Plasma (ionized gas)
  • Thermonuclear core
  • Outer convective surface
  • We see the photosphere, where the atmosphere becomes opaque
NSO

Solar magnetic field

The Sun is an ionized fluid!
Solar Dynamics Observatory

Solar magnetic field

The Sun is an ionized fluid!
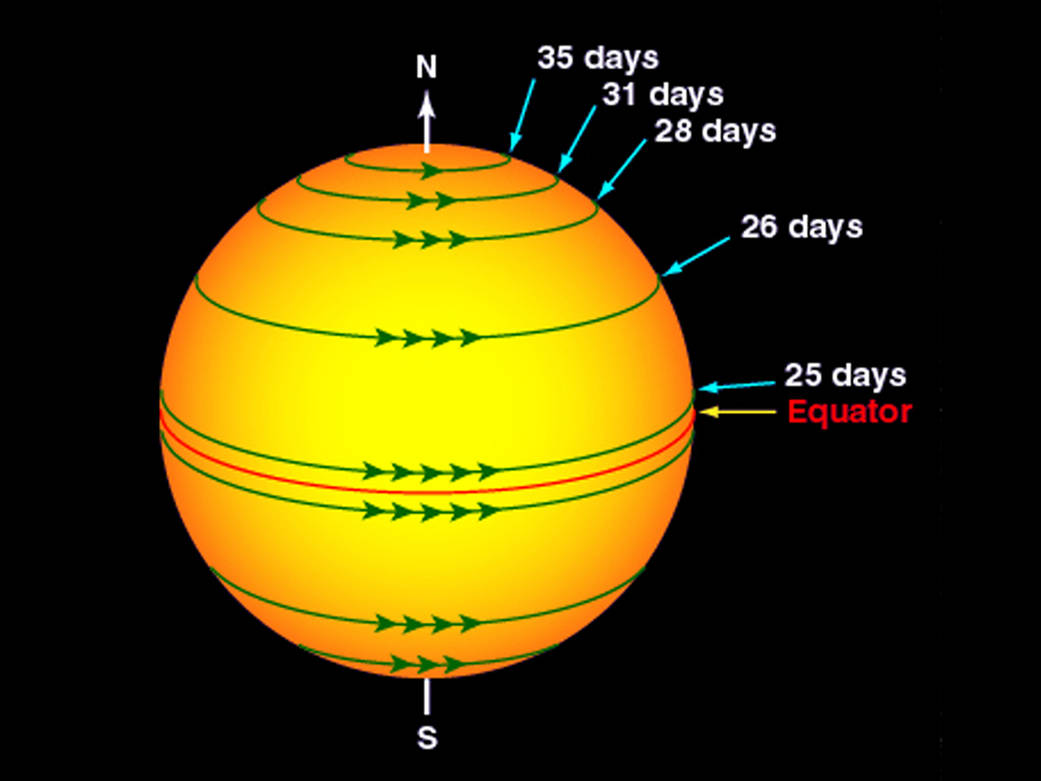
NASA / Wikimedia

Magnetic activity → sunspots

Magnetogram
Visible light intensity
Chromosphere
High magnetic activity → upwelling/downwelling → dark sunspots paired with brighter faculae (plages in chromosphere)
Solar Dynamics Observatory, Sept. 10 2024

Solar cycle

~11-year cycle between low and high solar activity
NASA

Solar cycle over time

Wikimedia
Solar irradiance varies by ~0.1% over the solar cycle

Sunspot variability and modern climate

Can we blame sunspots?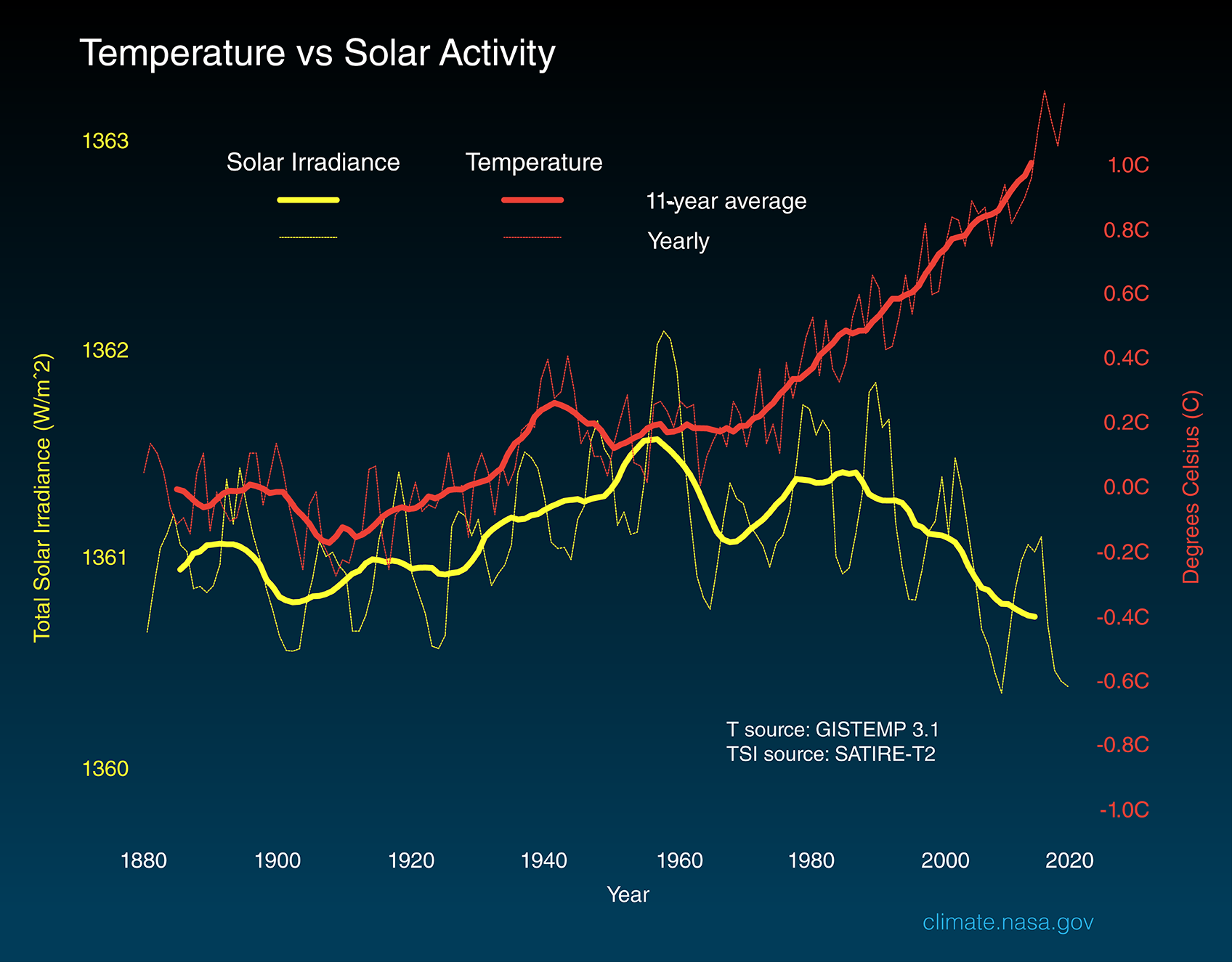
NASA

Lab this afternoon in MMS 273

Lab 1 due tomorrow (Friday) by 11:59pm

Next Week ()

  • Readings: Syllabus / Canvas
  • Meet with me on quantitative skills ASAP
  • Coming up: 🌎 Radiative 🌍 forcing 🌏